4 05 2017

close all;
clear;
f=5;         %5 hz frekans
A=1;        %sinyalin genliği
fs=20.*f;    %örnekleme frekansı sinyal frekansının 20 katı
ts=1/fs;    %örnekleme periyodu
t=0:ts:(10/f); % 0-2 sn arası 10 periyot (5hz için)

x=sin(2*pi*f*t); %5 hz sinüs sinyali
figure
subplot(2,3,1);
plot(t,x);
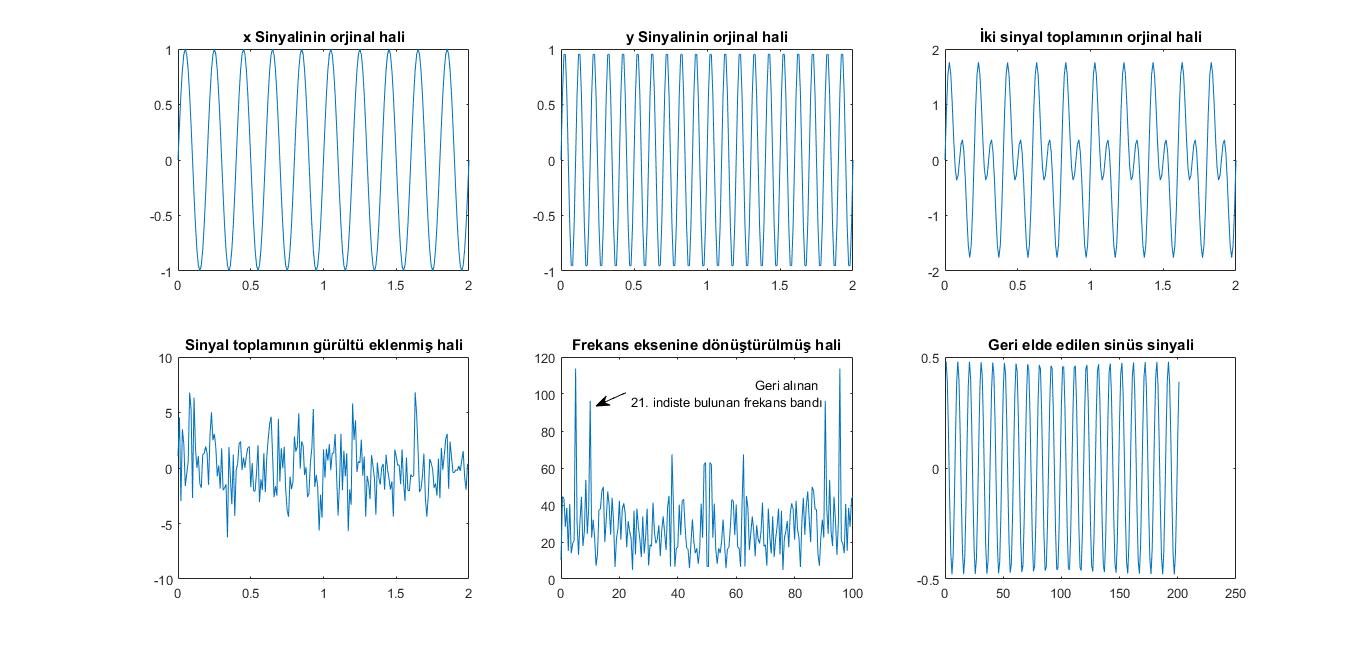
title(‘x Sinyalinin orjinal hali’)
%%

y=sin(2*pi*2*f*t);% 10 hz sinüs sinyali
subplot(2,3,2);
plot(t,y);
title(‘y Sinyalinin orjinal hali’)
%%

z=x+y;
subplot(2,3,3);
plot(t,z);
title(‘İki sinyal toplamının orjinal hali’)
%%

z=x+y + (2*randn(size(t))); %random gürültü eklendi
subplot(2,3,4);
plot(t,z);
title(‘Sinyal toplamının gürültü eklenmiş hali’)

%%
fft0=fft(z);
fft1=abs(fft0);

fv=0:(fs/(length(z)-1)):fs; %frekans vektörü oluşturuldu.
% fv = linspace(0,fs,length(x)); % Frekans vektörünü oluşturur. Bu da
% kullanılabilir.
subplot(2,3,5);
plot(fv,fft1);
title(‘Frekans eksenine dönüştürülmüş hali’)

%%
%sinyal geri kazanma, ters fourier dönüşümü
% Önce band geçiren filtreleme yapılıyor.
%fft1 21. indiste bulunan frekans bandı filtrelenerek alınıyor ve zaman
%domainine transfer ediliyor.
z0=zeros(1,length(fft1));
z0(21)=fft1(21);%fft1 dizisi içinde en yuksek değerlerin 11 ve 21. indislerde olduğu anlaşıldı.
z1=ifft(z0);
subplot(2,3,6);
plot(real(z1))
title(‘Geri elde edilen sinüs sinyali’)

VTIY ODEV YANITLARI (25/04/2017) VTIY Gerçek Zamanlı Sensör Değeri Okuma